Localization with a range finder

Localization via a range finder

In our last experiment, we simulated a robot with three color sensors pointed in different directions. In each of the tests, the robot easily localized itself. But in most robotics applications, robots often have distance data to its surroundings, instead of color information. We see this in simple robots that use ultrasonic range finders to detect walls and nearby objects. We also see this in complex platforms, e.g., self-driving cars often have rotating LIDAR(s) on top of the vehicle. This system maps the immediate neighborhood around the robot car. The LIDAR data output is typically a point cloud, indicating different points in the environment and their distances from the LIDAR. We will explore this range-based mechanism in a simplified simulation.

Simulation setup

We will not recreate a continuous point cloud. Instead, we will simply replace the color data from the three sensors in the previous post with distance information. We will also simplify the problem by assuming that a diagonal distance between cells is equal to the lateral or vertical distance between cells. This assumption is not an issue as long as the method of measurements is consistent when pre-storing map information and while navigating.

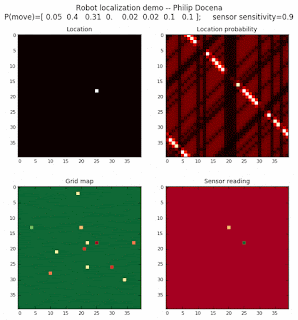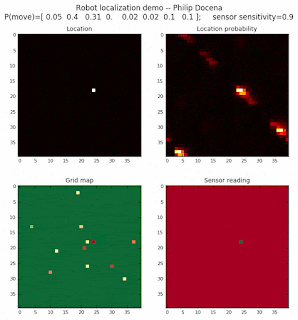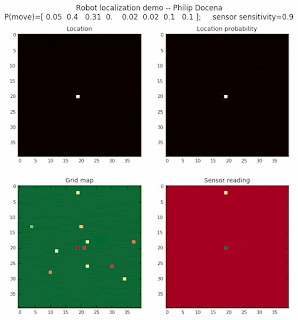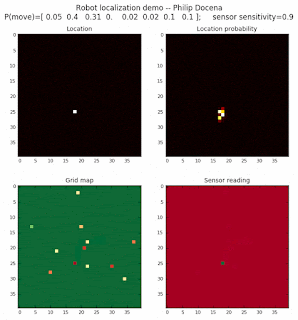
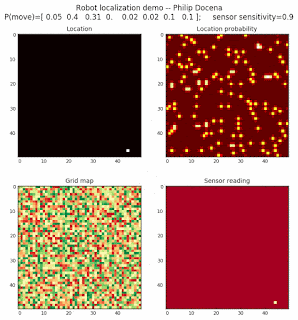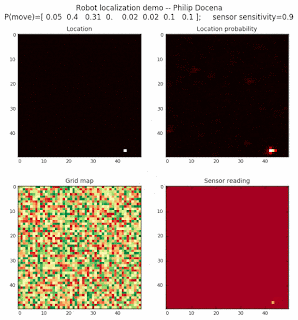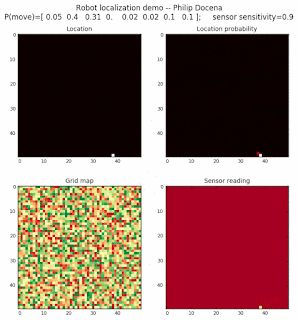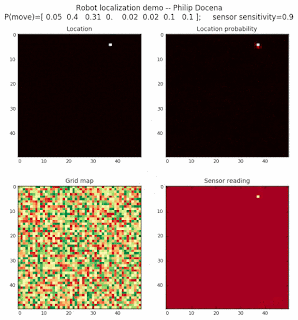
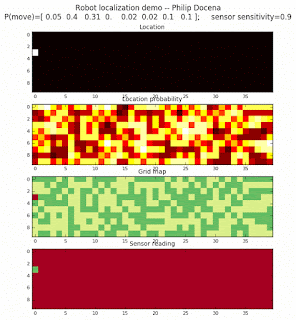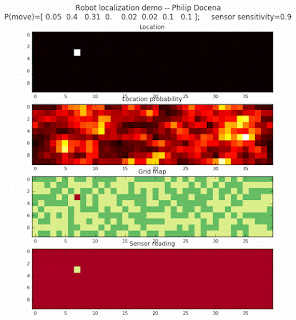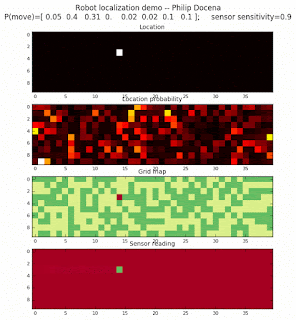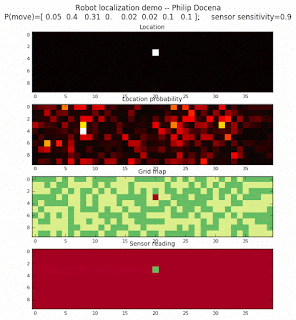
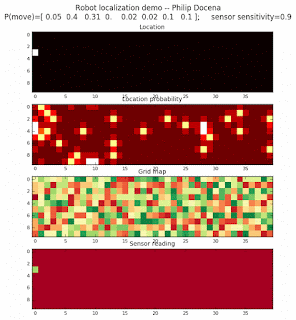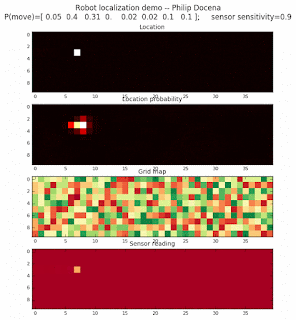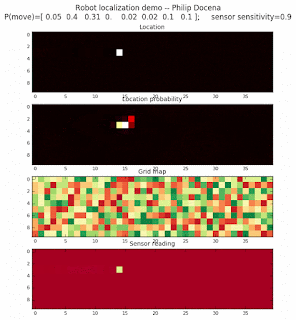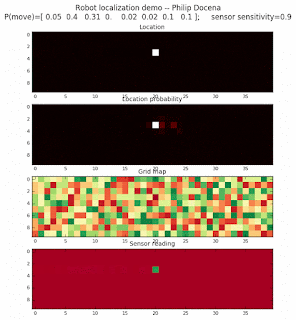
To show the changes in the distance data, we will make a slight change in the graph. We now put the location of the robot and the objects cells detected by the range finder in the first graph (upper left), and place the probability estimates on the lower right graph. The lower left remains the same, the map of the environment and the robot. On the upper right, we introduce a new graph where we plot (via a histogram) the detected distances for each of the three

Simulations

Our simulations will involve two runs, the first with 1 object type and the second with 2 object types. In theory, there should not be any difference in the localization between 1-object or 2-object runs since the range finder sensors cannot distinguish the object type, only its distance to the sensor. We will also test a low and high object density scenarios.

Low density runs

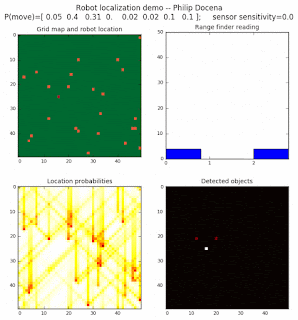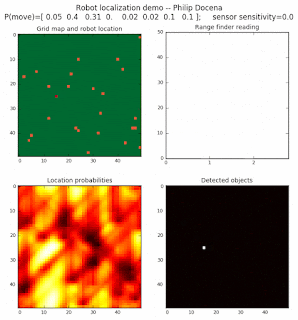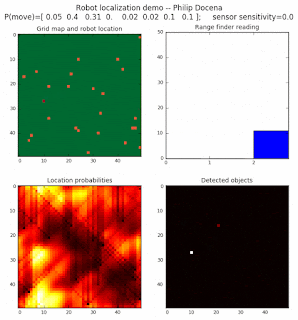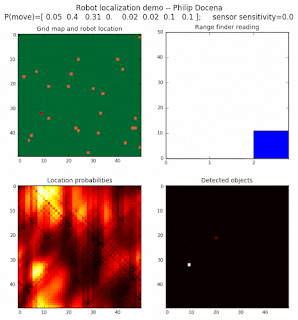
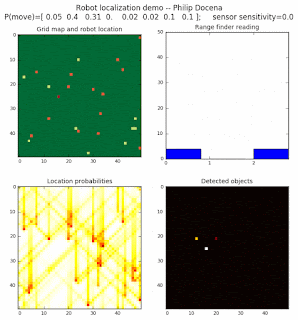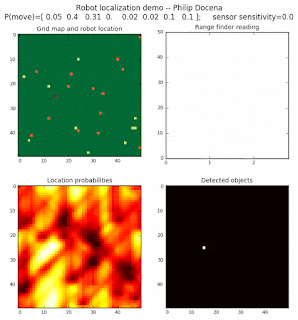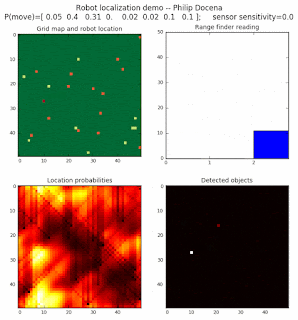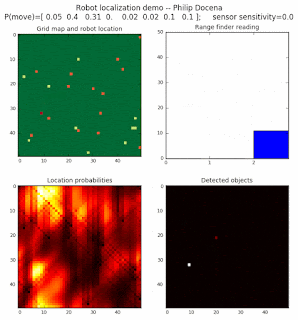
High density runs

We notice that the localization is not very precise and take many more iterations to reach a high-contrast prediction. This is expected. The number of distance possibilities that might match (or be a close match) to the current location is higher. In comparison, the very specific object type identity (via the color sensors) allows the algorithm to eliminate many cell locations as highly improbable. In a distance calculation, many more cell locations are likely locations, hence the spread out probabilities and lack of color contrast (compared to our previous simulations).

Improving the cell elimination

The problem with the above approach is that the many cells have distance calculation that are at least close to the distance measured by the range finders. Thus, they tend to maintain high probabilities as a potential robot location. One possible way to sharpen the guessing is to eliminate distance calculations that are less than a threshold away from the reported distance. This should quickly eliminate locations that are marginally viable. Let’s try this:

Low density runs

High density runs

Voila! We are able to quickly zoom in to the cells that are likely robot locations far quickly and with more contrast to neighboring cells.

Localization via landmarks

Our previous simulated robots have color sensors aimed down to detect the color of their current location in a map. Let’s show one that has color sensors aimed horizontally, to show a more realistic camera orientation. Our localization algorithm will therefore navigate using objects it encounters as localization landmarks.

Simulation setup

Let’s define our simulation parameters. For the most part, we will retain the modeling behavior from previous simulations, with some minor modifications.

Gridmap

We retain the same mechanics as before. The robot can move in any of four directions: left, right, up, and down. The robot has no heading orientation, so when it moves sideways, it does not rotate first. It simply moves sideways. The robot motion could be noisy, which means in some very rare instances, the robot might move diagonally. This is unlikely however. Its occurrence does not materially change the simulation. The robot moves over a cyclic gridmap, with each side continuing to the opposing edge. The gridmap is randomly populated with objects or structures.

Color sensors

We will design three color sensors that can read color at any distance with some accuracy. The sensor’s accuracy can change (can be modeled as less than perfect, as in previous simulations), but its accuracy remains the same over any distance. This is not a realistic representation --sensor accuracy, particularly color detection, weakens the farther the object being observed-- but good enough to show how localization in this manner would work. Changing the code to accommodate increasing sensor error with increasing distance is not hard, but unnecessary for a proof-of-concept. These sensors are fixed. They do not rotate when the robot changes direction.

Color sensor readout

The colors in each cell represent the color of the object/structure in that cell location (an object cell). The only exception is the color ‘green’, which we will use to denote ground, i.e., a ground cell and not a structure. The robot has three cameras, or color sensors: one aimed directly forward, one to the left at a 45 degree angle, and another one aimed 45 degrees to the right. Each sensor will detect the color of the first structure in its line-of-sight. Since ground is not at eye/sensor-level, the color sensors do not ‘see’ the green ground cells in its view path. The robot will detect the first non-ground structure, keeping in mind the cyclic nature of the gridmap. The structures detected by the three sensors are shown in the lower-right diagram during each iteration. For ease of coding, the robot can occupy the same cell as these objects (no collision detection).

Sensor diagram

On this diagram, the current robot location is identified as the ‘green’ cell. On a non-cyclic map, there should not be any highlighted cell below the current robot location, since all sensors are aimed up/forward. In our cyclic map, if the diagram shows a cell below the current robot location, it means one of the three sensors did not see a structure within the gridmap, and had to cycle through the opposing edge until it found a structure cell. We only cycle the sensor by one map width. If the sensor does not detect a structure after one cycle, the sensor reports ‘green’, the ground color. [This default color value is unnecessary, but I had to part the reading on some value.] Note that the robot has no information about how far these structures are relative to the robot. All the robot receives are three color information, one for each color sensor.

Simulations

Let’s run some simulations, varying the number of object types (number of different cell colors) and object density (total number of all objects in the gridmap).

1-object world

Let’s start with a world with only one type of object. We expect that this would take a little bit of time to localize. That said, a world with only one object type (two, including the ground cell) would be even more difficult to localize in our previous experiments with the single downward-looking color sensor. Intuitively, we would guess that the three-sensor model would work faster since it would eliminate more locations per iteration. We won't test this comparison however.

2-object world

Let’s do the same with a 2-object world, using roughly the same object density.

8-object world

Finally, let’s populate the robot world with eight types of objects, again maintaing approximately the same object density over the gridmap.

Low object-density world

We are also interested in localizing over a world where there are few landmarks. Let's repeat the above experiments, but with far fewer objects present.

1-object world

Let’s start with the 1-object test:

2-object world

Followed by the 2-object run:

8-object world

Finally, an 8-object low density test:

Closing thoughts

We showed a simplified model of a robot that uses cameras to detect objects, and use this information to localize itself. While the camera detection is crude --representing an object with a single color, assuming the camera only 'sees' one object at a time and does not model an expanding line-of-sight, accuracy at any distance is the same-- the mechanics remain applicable to a real-world application. Instead of identifying a color, an object or scene recognition system can process the camera stream and match the result to the map. Multiple cameras can add additional visual references to orient and localize a real robot.

In our next experiment, we will replace the color sensor with a distance sensor. Most navigation robots use a range finder to map its surroundings. Understanding visual cues and recognizing objects are still unreliable. Computer vision is hard, and processing images to generate a map is fundamentally more difficult than receiving raw distance data from a range finder. There is practically zero computing overhead with these sensors, and even cheap ultrasonic sensors have sufficient accuracy for simple applications. So it is time we model such a setup.

Localization over heterogeneous features, part 2

Localization under different environments, part 2

This is a continuation of the previous post on localization under heterogenous features (see here), where we made clear that localization appears faster with more distinctive features present in an environment. The assumption of course is that the robot sensor is capable of distinguishing all of these diverse features (i.e., colors) even if the sensor is not perfectly accurate.

Let’s make this analysis more definitive by doing away with our visual grid color interpretation. It is often hard to tell which of two similar cells is more ‘white-hot’, so let’s use the actual probabilities. We start with another simulation, this time over a 50x50 gridmap. We will run four different levels of feature diversity (2, 4, 8, and 16 objects in the environment), but only show the two extremes. Below are the simulations:

Probability plot

It is obvious that the probability assigned to the actual cell location is higher (more white-hot) than those from other locations as more object types are added to the environment. We should be able to confirm this by plotting the predicted probabilities at the actual cell location over several iterations for each run. Here’s the graph:

As predicted, we do see that the simulation with 16 objects tends to have higher probabilities calculated for the actual cell location at each iteration.

However, we should also compare the cell probability with the maximum probability possible for each iteration. There might be cells with even higher probabilities, which would lead us to conclude that those cells are the actual location(s). Let's explore this in the next graph.

Probability vs max probability

Let’s look at the ratio of the probability of the actual grid location against the maximum probability for any cell at each step. Here’s the graph:

From the graph above, it is hard to conclude that the 16-object example has any particular advantage. It does show that the simulations with more objects tend to reach a ratio of 1.0 quickly, suggesting that the probability at the actual cell location is calculated to be at least equal to the maximum probability possible during that iteration. But we do not know how many cells have this maximum value. In other words, we might have multiple 'best' candidate locations, and the actual cell location is only one of them.

Perhaps we are not looking at the correct ratio. If we think about it, we know that the 16-object simulation is better because the number of cells that are visually comparable to the color intensity of the actual cell is minimized. This means that the probability of the predicted location will tend to be higher compared to the average over the entire grid. Similarly, the predicted cells have very high contrast relative to neighboring cells. They are also highly concentrated, with just a few candidate locations, suggesting high predictive precision. This implies that we can apply some ratio using the cells that outperform the probability assigned to the actual cell location. Let's explore these thoughts below.

Probability vs average probability

To take advantage of contrast relative to all other cells, we look at the ratio of the probability of the actual grid location against the average probability for all cells at each step (including the actual cell location). Here’s the graph:

Number of cells equal to or better than actual location probability

As the localization gets more accurate, the number of candidate cell locations tend to decrease. With fewer cells identified as possible locations, the probabilities for all cells rise as a result. We can therefore count the number of high probability location and take the inverse. The higher the value of this ratio, the better. Its maximum value is 1.0 (100%). Let’s call this current-to-best-cells ratio:

Ratio of number of best predictions against all possible cells

We could also calculate a related ratio, where we calculate the ratio between the number of high probability cell locations and the total number of grid cells in the map. As the localization become more precise, the numerator will tend to decrease, causing the ratio to decrease to 1 over the total number of cells in the map. This is the same as the above, but expressed inversely and normalized with the total map size. Let’s call this best-cells-to-total ratio:

From the two ratios, we are able to extract the best (lowest/highest) localization with the 16-object simulation. We can also observe that localization tends to be faster with more objects. This is indicated by the earlier jump of the current-to-best-cells ratio on the 16-object run, followed by the 8-object run, and so on. There is also a limit to the best localization possible with fewer object types. This makes sense because if we have only a few features types, it would be difficult to pin down an exact location.

Let's put all these graphs together for easier comparison:

Closing thoughts

It is now very clear that the more heterogeneous the environment, assuming the algorithm is able to sense the disparate objects within such environment, the faster the localization algorithm would settle on a few cells, assigning far higher probabilities than the rest of the cells. We also observed that it is also more accurate, as shown by the maximum ratio reached by a 2-object simulation vs a 16-object simulation. The implication is that the versatility of the sensor used and the variety of objects detectable by such sensor in a particular environment are key to a fast and accurate localization.

Localization over heterogeneous features, part 1

Localization under different environments

In the previous post (here), we introduced a simple demonstration for discrete localization. Some of the examples did not clearly pinpoint a single location for the robot after the first 20 steps, although it did eliminate some locations as highly unlikely. With more iterations, the algorithm should be able to narrow down the possible locations to a few coordinates, perhaps even the actual robot location. Most of the incorrect location guesses were due to the imperfect sensor readings and the unreliable robot motion, modeled as probabilistic locations for each intended movement. In this post, we will evaluate if there are environments where the localization is faster.

The effect of environmental features diversity

In the previous experiments, a major cause for the slower localization was the limited number of distinct environmental features. We used a fairly uniform densities for only three types of observations, i.e., three different colors over the gridmap. It is therefore easy to mistake one location for another given a color reading, even after matching a chain of color readings. In some cases, even when the intervening step(s) decreased the probability of a wrong candidate location, the next step would increase the probabilities again --while the probabilistic movements made the correct candidate location less precise. This caused the localization to linger over incorrect locations for a few steps.

Simulating the effects of environmental features diversity

In this post, we explore if our hunch is correct: that an environment filled with more disparate features will allow a robot to localize quickly. Intuitively, this should be the case. A diverse environment allows a single observation to eliminate more candidate locations than would be possible in a more homogenous environment. In our simulation, if each cell was a different color, then a color reading would eliminate all but one cell, even with noisy robot motion, leading us to the correct cell location. If the color sensor is imprecise, the correct cell would still rise above its incorrect neighbors in a few steps.

We will model several environments using the same algorithm used in the previous post. We will vary the number of distinct features from 2, 4, 8, and 16. We can see the effect of these settings in the colors displayed on the grid map.

Demo 1a, all directions allowed, number of distinct features: 2

Demo 1b, all directions allowed, number of distinct features: 4

Demo 1c, all directions allowed, number of distinct features: 8

Demo 1d, all directions allowed, number of distinct features: 16

Let's also run several simulations on a left-to-right motion, as comparison to the previous post's experiments. We will also vary the diversity of features.

Demo 2a, left-to-right only, number of distinct features: 2

Demo 2b, left-to-right only, number of distinct features: 4

Demo 2c, left-to-right only, number of distinct features: 8

Demo 2d, left-to-right only, number of distinct features: 16

Closing thoughts

With these experiments, we established that the discrete localization algorithm can localize more quickly when the environment is more heterogenous. This also suggests that sensors that can detect different features are more useful in localizing than less discerning sensors, even when the latter are more accurate.

There are other experiments to explore. For example, does noisy motion affect localization in a diverse environment? In initial tests, in a highly chaotic map with small islands of cells (one or a couple of pixels) of the same color, a noisy motion leads to a harder time localizing, since practically any color could be reached in each step, so every cell tend to have some non-trivial probability. We will not explore this in detail at this time.

We could also model clusters of colors to reflect imprecise maps. In human terms, when we are inside a room, we can estimate that we are closer to one wall vs an opposing wall, but we would have to estimate if we are one fourth of the way, but would not know exactly (and we could be one-third or one-fifth closer to the wall). We can model this with color clusters in our map. Our intuition is that the probability will spread out across these clusters, but becoming more accurate as the robot detects a color change when traversing a cell cluster border. This is similar to being lost at sea without visible landmarks, but at least knowing you are in one of several island in the area when you get to any shore. This is indeed the case in initial experiments, which we will not pursue in more detail at this time.