Localization with a range finder

Localization via a range finder

In our last experiment, we simulated a robot with three color sensors pointed in different directions. In each of the tests, the robot easily localized itself. But in most robotics applications, robots often have distance data to its surroundings, instead of color information. We see this in simple robots that use ultrasonic range finders to detect walls and nearby objects. We also see this in complex platforms, e.g., self-driving cars often have rotating LIDAR(s) on top of the vehicle. This system maps the immediate neighborhood around the robot car. The LIDAR data output is typically a point cloud, indicating different points in the environment and their distances from the LIDAR. We will explore this range-based mechanism in a simplified simulation.

Simulation setup

We will not recreate a continuous point cloud. Instead, we will simply replace the color data from the three sensors in the previous post with distance information. We will also simplify the problem by assuming that a diagonal distance between cells is equal to the lateral or vertical distance between cells. This assumption is not an issue as long as the method of measurements is consistent when pre-storing map information and while navigating.

To show the changes in the distance data, we will make a slight change in the graph. We now put the location of the robot and the objects cells detected by the range finder in the first graph (upper left), and place the probability estimates on the lower right graph. The lower left remains the same, the map of the environment and the robot. On the upper right, we introduce a new graph where we plot (via a histogram) the detected distances for each of the three

Simulations

Our simulations will involve two runs, the first with 1 object type and the second with 2 object types. In theory, there should not be any difference in the localization between 1-object or 2-object runs since the range finder sensors cannot distinguish the object type, only its distance to the sensor. We will also test a low and high object density scenarios.

Low density runs

High density runs

We notice that the localization is not very precise and take many more iterations to reach a high-contrast prediction. This is expected. The number of distance possibilities that might match (or be a close match) to the current location is higher. In comparison, the very specific object type identity (via the color sensors) allows the algorithm to eliminate many cell locations as highly improbable. In a distance calculation, many more cell locations are likely locations, hence the spread out probabilities and lack of color contrast (compared to our previous simulations).

Improving the cell elimination

The problem with the above approach is that the many cells have distance calculation that are at least close to the distance measured by the range finders. Thus, they tend to maintain high probabilities as a potential robot location. One possible way to sharpen the guessing is to eliminate distance calculations that are less than a threshold away from the reported distance. This should quickly eliminate locations that are marginally viable. Let’s try this:

Low density runs

High density runs

Voila! We are able to quickly zoom in to the cells that are likely robot locations far quickly and with more contrast to neighboring cells.

Localization via landmarks

Our previous simulated robots have color sensors aimed down to detect the color of their current location in a map. Let’s show one that has color sensors aimed horizontally, to show a more realistic camera orientation. Our localization algorithm will therefore navigate using objects it encounters as localization landmarks.

Simulation setup

Let’s define our simulation parameters. For the most part, we will retain the modeling behavior from previous simulations, with some minor modifications.

Gridmap

We retain the same mechanics as before. The robot can move in any of four directions: left, right, up, and down. The robot has no heading orientation, so when it moves sideways, it does not rotate first. It simply moves sideways. The robot motion could be noisy, which means in some very rare instances, the robot might move diagonally. This is unlikely however. Its occurrence does not materially change the simulation. The robot moves over a cyclic gridmap, with each side continuing to the opposing edge. The gridmap is randomly populated with objects or structures.

Color sensors

We will design three color sensors that can read color at any distance with some accuracy. The sensor’s accuracy can change (can be modeled as less than perfect, as in previous simulations), but its accuracy remains the same over any distance. This is not a realistic representation --sensor accuracy, particularly color detection, weakens the farther the object being observed-- but good enough to show how localization in this manner would work. Changing the code to accommodate increasing sensor error with increasing distance is not hard, but unnecessary for a proof-of-concept. These sensors are fixed. They do not rotate when the robot changes direction.

Color sensor readout

The colors in each cell represent the color of the object/structure in that cell location (an object cell). The only exception is the color ‘green’, which we will use to denote ground, i.e., a ground cell and not a structure. The robot has three cameras, or color sensors: one aimed directly forward, one to the left at a 45 degree angle, and another one aimed 45 degrees to the right. Each sensor will detect the color of the first structure in its line-of-sight. Since ground is not at eye/sensor-level, the color sensors do not ‘see’ the green ground cells in its view path. The robot will detect the first non-ground structure, keeping in mind the cyclic nature of the gridmap. The structures detected by the three sensors are shown in the lower-right diagram during each iteration. For ease of coding, the robot can occupy the same cell as these objects (no collision detection).

Sensor diagram

On this diagram, the current robot location is identified as the ‘green’ cell. On a non-cyclic map, there should not be any highlighted cell below the current robot location, since all sensors are aimed up/forward. In our cyclic map, if the diagram shows a cell below the current robot location, it means one of the three sensors did not see a structure within the gridmap, and had to cycle through the opposing edge until it found a structure cell. We only cycle the sensor by one map width. If the sensor does not detect a structure after one cycle, the sensor reports ‘green’, the ground color. [This default color value is unnecessary, but I had to part the reading on some value.] Note that the robot has no information about how far these structures are relative to the robot. All the robot receives are three color information, one for each color sensor.

Simulations

Let’s run some simulations, varying the number of object types (number of different cell colors) and object density (total number of all objects in the gridmap).

1-object world

Let’s start with a world with only one type of object. We expect that this would take a little bit of time to localize. That said, a world with only one object type (two, including the ground cell) would be even more difficult to localize in our previous experiments with the single downward-looking color sensor. Intuitively, we would guess that the three-sensor model would work faster since it would eliminate more locations per iteration. We won't test this comparison however.

2-object world

Let’s do the same with a 2-object world, using roughly the same object density.

8-object world

Finally, let’s populate the robot world with eight types of objects, again maintaing approximately the same object density over the gridmap.

Low object-density world

We are also interested in localizing over a world where there are few landmarks. Let's repeat the above experiments, but with far fewer objects present.

1-object world

Let’s start with the 1-object test:

2-object world

Followed by the 2-object run:

8-object world

Finally, an 8-object low density test:

Closing thoughts

We showed a simplified model of a robot that uses cameras to detect objects, and use this information to localize itself. While the camera detection is crude --representing an object with a single color, assuming the camera only 'sees' one object at a time and does not model an expanding line-of-sight, accuracy at any distance is the same-- the mechanics remain applicable to a real-world application. Instead of identifying a color, an object or scene recognition system can process the camera stream and match the result to the map. Multiple cameras can add additional visual references to orient and localize a real robot.

In our next experiment, we will replace the color sensor with a distance sensor. Most navigation robots use a range finder to map its surroundings. Understanding visual cues and recognizing objects are still unreliable. Computer vision is hard, and processing images to generate a map is fundamentally more difficult than receiving raw distance data from a range finder. There is practically zero computing overhead with these sensors, and even cheap ultrasonic sensors have sufficient accuracy for simple applications. So it is time we model such a setup.

Discrete localization demo

Simulated robot localization demo

My previous posts have been about machine learning techniques. Let’s do something different and get into non-ML AI this time, into the world of robotics.

Save a lost friend

Imagine trying to locate a friend lost in unrecognizable terrain with no distinct landmarks. Your friend has an altimeter on his phone, but no GPS or any other navigational tool. His phone can send text/call otherwise. You are trying to find him by using a contour map. He can give you the elevation at his current location, which he does every minute while resting. Being smart, you thought it would be easier to ‘guess’ her location if he walks towards the sun. You are unsure about his exact hiking speed, and hence his exact displacement/location after he walks for each minute between his elevation updates. But you have a good estimate of how much farther a normal person would be when walking in this terrain per minute –as a proxy for your friend's walking abilities– including estimates of minor deviations away from an intended straight line walking path. Can you estimate his location?

A simple solution…

Logic and a little math tell us we can do this. We simply need to match the elevation updates with possible routes that point towards the sun. We could start with all elevations in the contour map that match her first elevation status. Then eliminate the ones that do not match the second elevation status along lines that point towards the sun. We continue doing this for a series of elevation updates, and after some time, as long as she goes through elevation changes now and then as she walks, we should be able to eliminate all but one location.

… complicated by uncertainties

But how do we handle the uncertainty introduced by the walking estimates, the reliability of the altimeter, or the accuracy of the map itself? The solution remains the same. We simply use more probabilities. And we can use AI techniques to solve this. Note that this is not strictly an AI problem, but it is a basic problem in AI and robotics.

Robot localization

This example is similar to how robots orient themselves in a known environment. The robot in our analogy has a map and a sensor. It knows where it is going directionally. Its first job is to locate itself in the map. This is called localization. It has to keep on estimating its location as it moves through this environment while accounting for tiny but accumulating errors in its movement, including possible sensor errors because sensors in the real world are not perfect. The best situation is a perfect sensor and exact motion calculations, but in reality these are always inaccurate. Optical sensors might be muddied or affected by available light sources. Movement is inexact because a motor command is translated with errors, perhaps because the motor is running out of juice, or wearing out, the wheels are slipping against the ground, and son on. In fact, even if we give the robot its precise starting coordinates, and work from there, we would still likely lose track of its next location due to these errors. The good thing is that they can be empirically estimated well enough to narrow our search.

Localization simulation

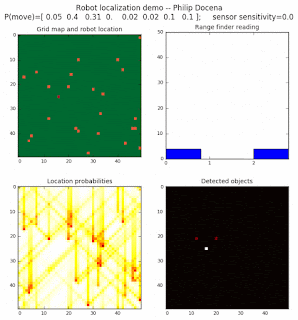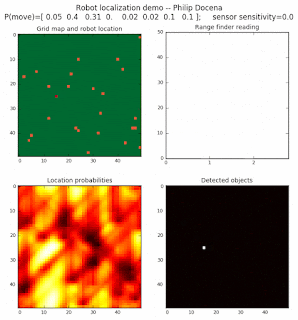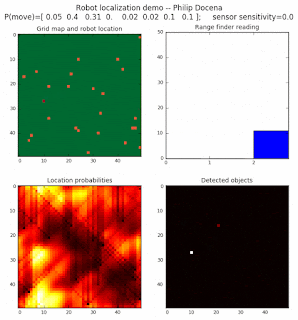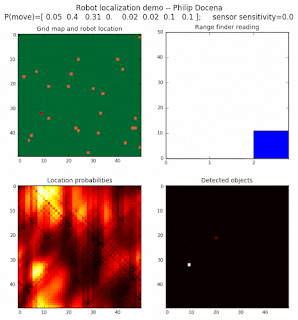
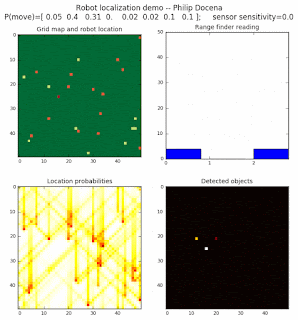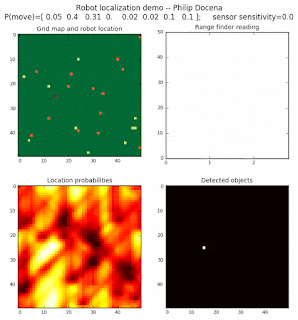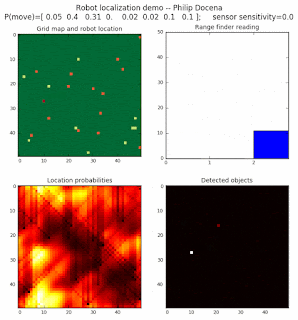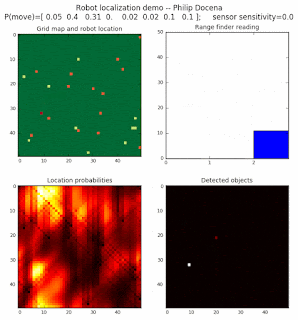
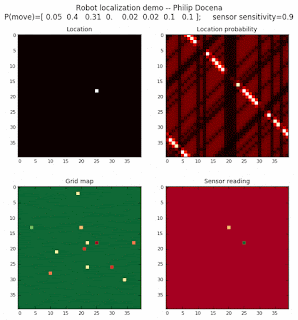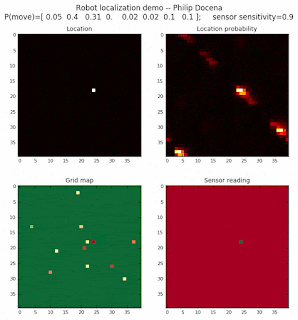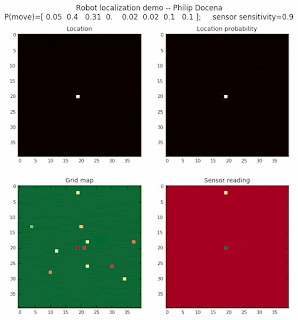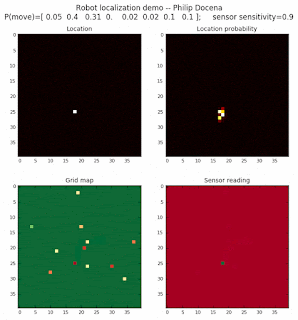
Below are an examples of how this could be done. The first graph is the location of the robot. The second is the current estimate of possible locations, shown as a heat map where high temperature (white-hot) means higher probability for that cell to be the robot location. The third graph is the environment, represented as a grid map of different colors. The fourth graph shows what the single sensor detects (the color of the current location). The fourth graph does not provide any X-Y coordinates to the localization algorithm. We just show the coordinates to help confirm that it matches the gridmap.

This example simulates a ‘robot’ that has wheels that are unreliable. For every movement, it could end up in different neighboring cell locations. It might not even move, or it might veer off, with different amounts of probability (which I assign pre-run). The robot's movement is randomly generated, with a bias towards continuing its current trajectory (not immediate backtracking, to make the localization faster). The variety of colors in the environment is also randomly generated, via a pre-run setting on color densities. The gridmap loops around itself in all directions, a common practice in simple simulations to minimize bounds checking code. This simplication sometimes prevents the algorithm from settling on a single stable localization.

The movement probabilities is given as P(move) in the graph, where the array P(move) is [current location; one cell forward; two cells forward; three cells forward; one cell forward, veer left; one cell forward, veer right; two cells forward, veer left; two cells forward, veer right].

We also model an imperfect color sensor. For these runs, we keep it as 0.9 --that is, for each color reading, it is 90% likely that the sensor detected the correct color, and a 10% likelihood that it failed and the cell is in fact a different color. Intuitively, we expect that the robot with an imperfect sensor will have a harder time finding itself accurately if neighboring cells have different colors. The worse the sensor, the harder the search.

The simulations below are limited to approximately 20 steps to minimize the GIF file size. Each step is made up of two sub-steps: a sensing step where the robot determines the color of its current grid cell, and a movement step where the robot moves based on a pre-generated random sequence. Notice that the probabilities become more precise with each color sensing step as the robot determines more exactly where it might be, and become less precise with each movement, because the robot has to assume multiple locations due to its 'faulty' wheels.

Demo 1A: box map, multi-directional movement, probabilistic motion, seed=0

The first demo allows the robot to move in any of four directions (left, right, up, down).

Demo 1B: box map, multi-directional movement, probabilistic motion, seed 1

The second demo is similar to the first, but with the robot following a different set of randomly generated movements.

Demo 1C: rectangle map, left-to-right movement only, seed 0

The third demo below restricts the robot to move only from left-to-right.

Demo 1D: rectangle map, left-to-right movement only, seed 1

The fourth demo is similar to the third, but with a different initial robot location.

Localization theory

This is based on the Udacity/Georgia Tech lecture on localization (the Markov/discrete variety, the simplest kind of localization), under AI for Robotics taught by Prof. Sebastian Thrun. He is famous for Stanley, the Stanford-entered autonomous car that won the DARPA Grand Driving Challenge in 2005. Thrun went on to work on Google’s self-driving car effort. His work, along with those of competing teams, became the lynchpin for today’s autonomous driving cars.

The theory is actually as simple as we described it above. It is a series of measurements and updating probabilities until most locations are eliminated as unlikely. As the robot moves, we just spread out to its possible locations. As we stop and sense the color of the current grid, we then update probabilities, penalizing those that do not match and increasing those that do. In theory, the location estimates are adjusted based on pre-established movement probabilities. In other words, if a robot was given an order to move its motors, there is an assumption of its range of possible motion/translation in the real world. This could also be fully replaced by a step to read inertial sensors, then build the probabilities based on the empirical probabilities of these inertial sensors. In other words, it will just be a series of sensor readings: read color sensor, read inertial sensor, read color sensor, and so on, independent of the motor commands.

Experiments with more precision

With better mechanicals and motion controls, we can make the robot movement more precise. In our simulation, let’s presume that we now have a robot that perfectly goes straight (no left-right deviations), but still has some errors with random wheel slippage. We can model this below. Notice that the spread of probabilities on each motion step is now purely along the axis of motion. We expect that we can find the robot more quickly than in the above example, and we do. It might be a little bit difficult to notice the color contrasts on the heatmap, but the algorithm can in fact calculate the location probabilities more precisely at each step.

The simulations below were done on exactly the same settings as those above, except for the P(move) probabilities, as shown in the graph title. We still have motion unreliability, but we restrict it to 0-3 cells directly in front of the robot.

Demo 2A: no side slip, box map, multi-directional movement, seed 0

Demo 2B: no side slip, rectangle map, left-to-right movement only, seed 0

Demo 2C: no side slip, small map A, left-to-right movement only, seed 0

Demo 2D: no side slip, small map B, left-to-right movement only, seed 0

This could be easily adopted –or rather I am very curious if it could be adopted easily-- to actual robots running over colored tiles, i.e., LEGO Mindstorms, which I will leave as a future project. We can also appreciate that this can be easily scaled to more sophisticated sensors and maps, e.g., a simple non-GPS drone navigation system using a local overhead map, and the sensor probabilities can be based on matching map features taken by a drone camera.

Closing thoughts

With the demo code that generated the above demo animation, I tested and produced interesting results on the accuracy tradeoffs between the two sensor probabilities (the color detector vs. the motion detector), and how the localization prediction behaves under different color densities and number of colors. We will not explore these results here as there are more interesting things to pursue on discrete localization.