Localization with a range finder

Localization via a range finder

In our last experiment, we simulated a robot with three color sensors pointed in different directions. In each of the tests, the robot easily localized itself. But in most robotics applications, robots often have distance data to its surroundings, instead of color information. We see this in simple robots that use ultrasonic range finders to detect walls and nearby objects. We also see this in complex platforms, e.g., self-driving cars often have rotating LIDAR(s) on top of the vehicle. This system maps the immediate neighborhood around the robot car. The LIDAR data output is typically a point cloud, indicating different points in the environment and their distances from the LIDAR. We will explore this range-based mechanism in a simplified simulation.

Simulation setup

We will not recreate a continuous point cloud. Instead, we will simply replace the color data from the three sensors in the previous post with distance information. We will also simplify the problem by assuming that a diagonal distance between cells is equal to the lateral or vertical distance between cells. This assumption is not an issue as long as the method of measurements is consistent when pre-storing map information and while navigating.

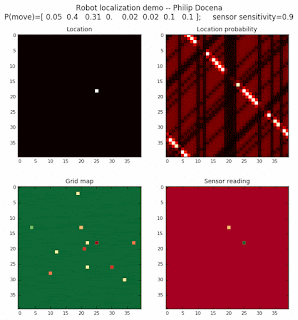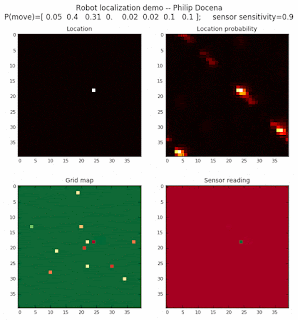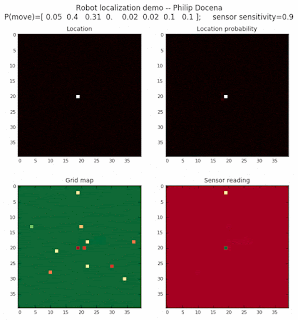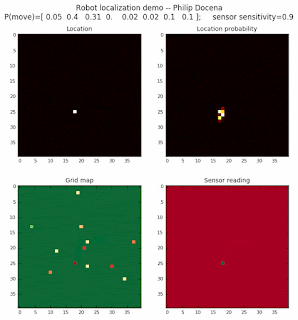
To show the changes in the distance data, we will make a slight change in the graph. We now put the location of the robot and the objects cells detected by the range finder in the first graph (upper left), and place the probability estimates on the lower right graph. The lower left remains the same, the map of the environment and the robot. On the upper right, we introduce a new graph where we plot (via a histogram) the detected distances for each of the three

Simulations

Our simulations will involve two runs, the first with 1 object type and the second with 2 object types. In theory, there should not be any difference in the localization between 1-object or 2-object runs since the range finder sensors cannot distinguish the object type, only its distance to the sensor. We will also test a low and high object density scenarios.

Low density runs

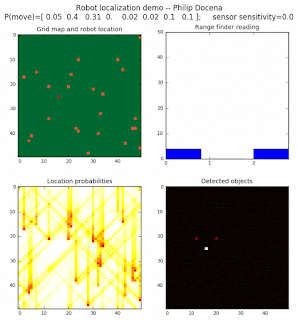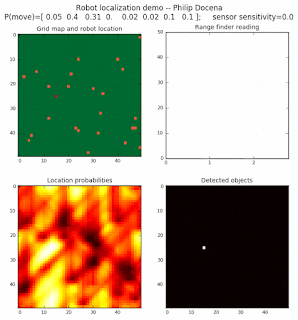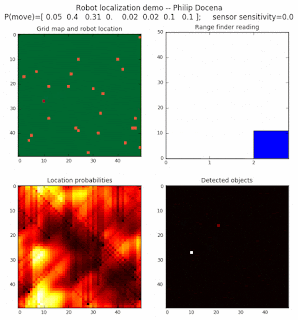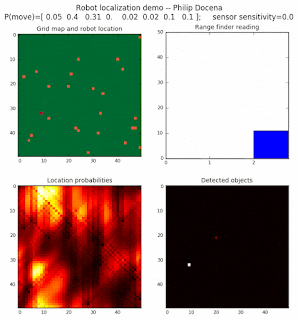
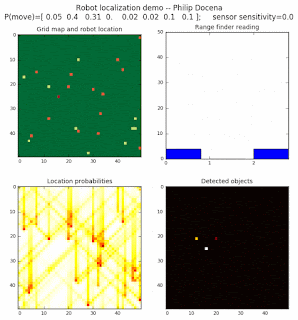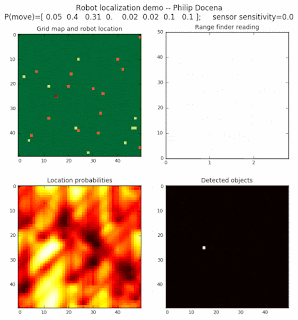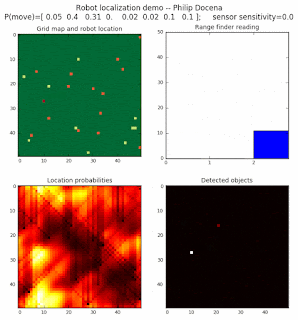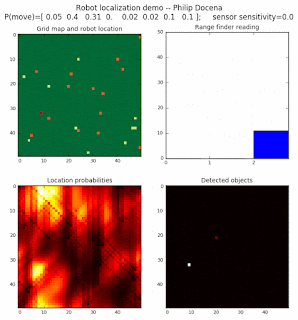
High density runs

We notice that the localization is not very precise and take many more iterations to reach a high-contrast prediction. This is expected. The number of distance possibilities that might match (or be a close match) to the current location is higher. In comparison, the very specific object type identity (via the color sensors) allows the algorithm to eliminate many cell locations as highly improbable. In a distance calculation, many more cell locations are likely locations, hence the spread out probabilities and lack of color contrast (compared to our previous simulations).

Improving the cell elimination

The problem with the above approach is that the many cells have distance calculation that are at least close to the distance measured by the range finders. Thus, they tend to maintain high probabilities as a potential robot location. One possible way to sharpen the guessing is to eliminate distance calculations that are less than a threshold away from the reported distance. This should quickly eliminate locations that are marginally viable. Let’s try this:

Low density runs

High density runs

Voila! We are able to quickly zoom in to the cells that are likely robot locations far quickly and with more contrast to neighboring cells.

Localization via landmarks

Our previous simulated robots have color sensors aimed down to detect the color of their current location in a map. Let’s show one that has color sensors aimed horizontally, to show a more realistic camera orientation. Our localization algorithm will therefore navigate using objects it encounters as localization landmarks.

Simulation setup

Let’s define our simulation parameters. For the most part, we will retain the modeling behavior from previous simulations, with some minor modifications.

Gridmap

We retain the same mechanics as before. The robot can move in any of four directions: left, right, up, and down. The robot has no heading orientation, so when it moves sideways, it does not rotate first. It simply moves sideways. The robot motion could be noisy, which means in some very rare instances, the robot might move diagonally. This is unlikely however. Its occurrence does not materially change the simulation. The robot moves over a cyclic gridmap, with each side continuing to the opposing edge. The gridmap is randomly populated with objects or structures.

Color sensors

We will design three color sensors that can read color at any distance with some accuracy. The sensor’s accuracy can change (can be modeled as less than perfect, as in previous simulations), but its accuracy remains the same over any distance. This is not a realistic representation --sensor accuracy, particularly color detection, weakens the farther the object being observed-- but good enough to show how localization in this manner would work. Changing the code to accommodate increasing sensor error with increasing distance is not hard, but unnecessary for a proof-of-concept. These sensors are fixed. They do not rotate when the robot changes direction.

Color sensor readout

The colors in each cell represent the color of the object/structure in that cell location (an object cell). The only exception is the color ‘green’, which we will use to denote ground, i.e., a ground cell and not a structure. The robot has three cameras, or color sensors: one aimed directly forward, one to the left at a 45 degree angle, and another one aimed 45 degrees to the right. Each sensor will detect the color of the first structure in its line-of-sight. Since ground is not at eye/sensor-level, the color sensors do not ‘see’ the green ground cells in its view path. The robot will detect the first non-ground structure, keeping in mind the cyclic nature of the gridmap. The structures detected by the three sensors are shown in the lower-right diagram during each iteration. For ease of coding, the robot can occupy the same cell as these objects (no collision detection).

Sensor diagram

On this diagram, the current robot location is identified as the ‘green’ cell. On a non-cyclic map, there should not be any highlighted cell below the current robot location, since all sensors are aimed up/forward. In our cyclic map, if the diagram shows a cell below the current robot location, it means one of the three sensors did not see a structure within the gridmap, and had to cycle through the opposing edge until it found a structure cell. We only cycle the sensor by one map width. If the sensor does not detect a structure after one cycle, the sensor reports ‘green’, the ground color. [This default color value is unnecessary, but I had to part the reading on some value.] Note that the robot has no information about how far these structures are relative to the robot. All the robot receives are three color information, one for each color sensor.

Simulations

Let’s run some simulations, varying the number of object types (number of different cell colors) and object density (total number of all objects in the gridmap).

1-object world

Let’s start with a world with only one type of object. We expect that this would take a little bit of time to localize. That said, a world with only one object type (two, including the ground cell) would be even more difficult to localize in our previous experiments with the single downward-looking color sensor. Intuitively, we would guess that the three-sensor model would work faster since it would eliminate more locations per iteration. We won't test this comparison however.

2-object world

Let’s do the same with a 2-object world, using roughly the same object density.

8-object world

Finally, let’s populate the robot world with eight types of objects, again maintaing approximately the same object density over the gridmap.

Low object-density world

We are also interested in localizing over a world where there are few landmarks. Let's repeat the above experiments, but with far fewer objects present.

1-object world

Let’s start with the 1-object test:

2-object world

Followed by the 2-object run:

8-object world

Finally, an 8-object low density test:

Closing thoughts

We showed a simplified model of a robot that uses cameras to detect objects, and use this information to localize itself. While the camera detection is crude --representing an object with a single color, assuming the camera only 'sees' one object at a time and does not model an expanding line-of-sight, accuracy at any distance is the same-- the mechanics remain applicable to a real-world application. Instead of identifying a color, an object or scene recognition system can process the camera stream and match the result to the map. Multiple cameras can add additional visual references to orient and localize a real robot.

In our next experiment, we will replace the color sensor with a distance sensor. Most navigation robots use a range finder to map its surroundings. Understanding visual cues and recognizing objects are still unreliable. Computer vision is hard, and processing images to generate a map is fundamentally more difficult than receiving raw distance data from a range finder. There is practically zero computing overhead with these sensors, and even cheap ultrasonic sensors have sufficient accuracy for simple applications. So it is time we model such a setup.